El Plano de Coordenadas
Objetivos de Aprendizaje
· Graficar pares ordenados en un plano de coordenadas.
· Dado un par ordenado, determina su cuadrante.
Introducción
El plano de coordenadas se desarrolló hace cientos de años y fue refinado por el matemático Francés René Descartes. En su honor, se le conoce también como sistema de coordenadas Cartesianas. El plano de coordenadas puede usarse para graficar puntos y rectas. Este sistema nos permite describir relaciones algebraicas de una manera visual, y también nos ayuda a interpretar conceptos algebraicos.
Conociendo el Plano de Coordenadas
Seguramente ya has usado el plano de coordenadas. Por ejemplo, ¿alguna vez has usado la cuadrícula de un mapa para encontrar la posición de un objeto? (Esto se hace también con mapas de carreteras.)

Este “mapa” usa una cuadrícula horizontal y vertical para describir información sobre la localización de un objeto. Observa que las letras A-F se enumeran en la parte superior, y los números 1-6 se enumeran a lo largo del borde izquierdo. La localización general de cualquier objeto en este mapa puede encontrarse usando la letra y el número de su cuadrícula. Por ejemplo, puedes encontrar el objeto que existe en el cuadro “4F” moviendo tu dedo sobre la horizontal de la letra F y luego hacia abajo para llegar a la línea 4. Encontrarás un disco azul en este lugar del mapa.
El plano de coordenadas tiene elementos similares a los de la cuadrícula de arriba. Consiste en un eje horizontal y un eje vertical, líneas numeradas que se intersectan en ángulos rectos. (Son perpendiculares una con la otra.)
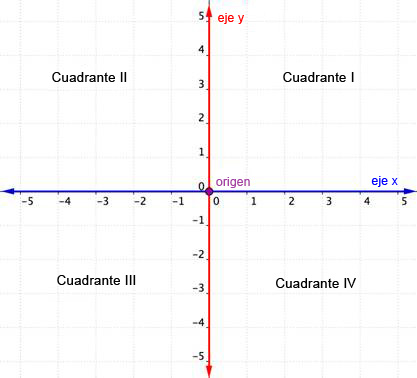
El eje horizontal en el plano de coordenadas se llama eje-x. El eje vertical se llama eje-y. El punto en el que los dos ejes se intersectan se llama origen. El origen está en el 0 del eje-x y del eje-y.
La intersección de los ejes x y y dividen el plano coordenado en cuatro secciones. Estas cuatro secciones se llaman cuadrantes. Los cuadrantes se nombran usando números Romanos I, II, III, IV empezando con el cuadrante superior derecho y moviéndose en contra de las manecillas del reloj.
Los puntos en el plano de coordenadas se describen usando pares ordenados. Un par ordenado te dice la localidad de un punto relacionándola con el eje-x (el primer valor del par ordenado) y con el eje-y (el segundo valor del par ordenado).
En un par ordenado, como (x, y), el primer valor se llama coordenada-x y el segundo valor es la coordenada-y. Observa que la coordenada-x se enlista antes de la coordenada-y. Como el origen tiene una coordenada-x de 0 y una coordenada-y de 0, su par ordenado se escribe (0, 0).
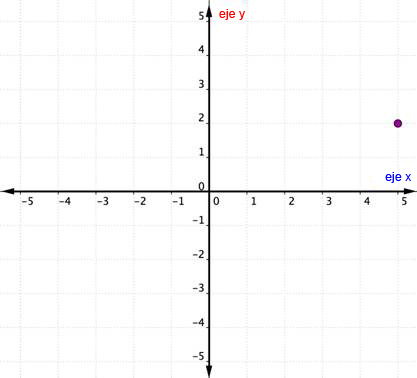
Considera el punto siguiente.
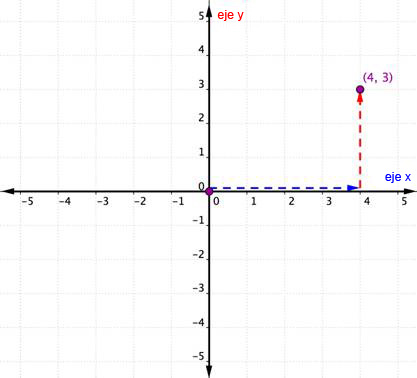
Para identificar la localización de este punto, empieza en el origen (0, 0) y muévete hacia la derecha sobre el eje-x hasta que llegues debajo del punto. Observa la etiqueta en el eje-x. El 4 indica que, desde el origen, te has movido 4 unidades a la derecha sobre el eje-x. Esta es la coordenada-x, el primer número del par ordenado.
Desde el 4 en el eje-x muévete hacia arriba hasta el punto y anota el número con el que se alinea en el eje-y. El 3 indica que, después de dejar el eje-x, subiste 3 unidades en la dirección vertical, la dirección del eje-y. Este número es la coordenada-y, el segundo número del par ordenado. Con una coordenada-x de 4 y una coordenada-y de 3, tienes el par ordenado (4, 3).
Veamos otro ejemplo.
| Ejemplo | ||
| Problema | Describir el punto mostrado como un par ordenado. | |
|
|
| |
|
| (5, y) | Empieza en el origen y muévete sobre el eje-x. Este es la coordenada-x y se escribe primero en el par ordenado. |
|
| (5, 2) | Muévete del 5 hacia arriba y lee el número en el eje-y. Este es la coordenada-y y se escribe segundo en el par ordenado. |
| Respuesta | El punto mostrado como un par ordenado es (5, 2). | |
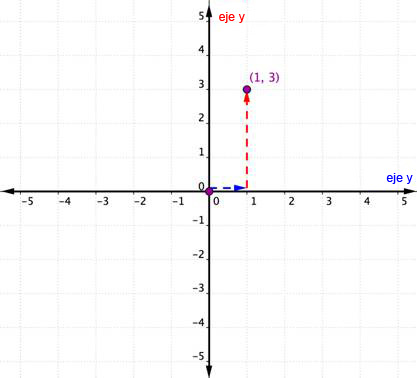
Ahora que sabes cómo usar los ejes x y y, puedes graficar un par ordenado. Pero recuerda, ambos procesos empiezan en el origen — ¡el inicio! El ejemplo siguiente muestra cómo graficar el par ordenado (1, 3).
| Ejemplo | ||
| Problema | Graficar el punto (1, 3). | |
|
|
| |
|
| La coordenada-x es 1 porque aparece al principio del par ordenado. Empieza en el origen y muévete una distancia de 1 unidad en la dirección positiva (hacia la derecha) desde el origen sobre el eje-x. | La coordenada-y es 3 porque aparece segundo en el par ordenado. Desde aquí, muévete una distancia de 3 unidades en la dirección positiva (hacia arriba). Si miras el eje-y, debes alinearte con el 3 en ese eje. |
| Respuesta | Dibuja un punto en esta localidad y etiquétalo (1, 3). | |
En el ejemplo anterior, las coordenadas x y y fueron positivas. Cuando una (o las dos) coordenadas de un par ordenado es negativa, necesitarás moverte en la dirección negativa sobre los ejes. Considera el ejemplo siguiente en el cual ambas coordenadas son negativas.
| Ejemplo | ||
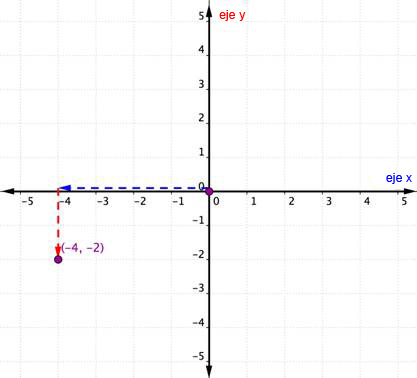
| Problema | Graficar el punto (−4, −2). | |
|
|
| |
|
| La coordenada-x es −1 porque aparece al principio del par ordenado. Empieza en el origen y muévete 4 unidades en la dirección negativa (hacia la izquierda) desde el origen sobre el eje-x. | La coordenada-y es −2 porque aparece segundo en el par ordenado. Ahora muévete 2 unidades en la dirección negativa (hacia abajo). Si miras el eje-y, debes alinearte con el −2 en ese eje. |
| Respuesta | Dibuja un punto en esta localidad y etiquétalo (−4, −2). | |
Los pasos para graficar un punto se resumen a continuación.
| Pasos para Graficar un Par Ordenado (x, y) en el Plano de Coordenadas o Determinar la coordenada-x. Empezando en el origen, muévete horizontalmente, la dirección del eje-x, la distancia dada por la coordenada-x. Si la coordenada-x es positiva, muévete a la derecha, si la coordenada-x es negativa, muévete a la izquierda. o Determinar la coordenada-y. Empezando en la coordenada-x, muévete verticalmente, la dirección del eje-y, la distancia dada por la coordenada-y. Si la coordenada-y es positiva, muévete hacia arriba, si la coordenada-y es negativa, muévete hacia abajo. Etiqueta el punto con el par ordenado.
|
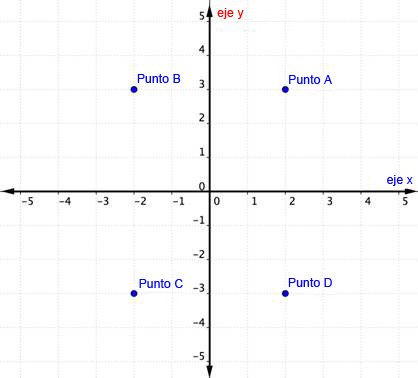
| ¿Qué punto representa el par ordenado (−2, 3)?
|
Los pares ordenados de un cuadrante particular comparten ciertas características. Observa cada cuadrante de la gráfica siguiente. ¿Qué notas sobre los signos de las coordenadas x y y de los puntos de cada cuadrante?
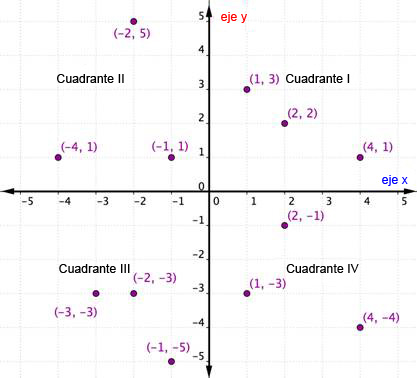
En cada cuadrante, los signos de las coordenadas x y y de cada par ordenado son los mismos. También siguen un patrón, que se detalla en la tabla siguiente.
| Cuadrante | Forma General del Punto en Este Cuadrante | Ejemplo | Descripción |
| I | (+, +) | (5, 4) | Empezando en el origen, sigue el eje-x en la dirección positiva (derecha) y sobre el eje-y en la dirección positiva (arriba). |
| II | (−, +) | (−5, 4) | Empezando en el origen, sigue el eje-x en la dirección negativa (izquierda) y sobre el eje-y en la dirección positiva (arriba). |
| III | (−, −) | (−5, −4) | Empezando en el origen, sigue el eje-x en la dirección negativa (izquierda) y sobre el eje-y en la dirección negativa (abajo). |
| IV | (+, −) | (5, −4) | Empezando en el origen, sigue el eje-x en la dirección positiva (derecha) y sobre el eje-y en la dirección negativa (abajo). |
Una vez que conoces los cuadrantes del plano de coordenadas, puedes determinar el cuadrante de un par ordenado sin siquiera ver la gráfica. Aquí hay otra forma de pensar en esto.
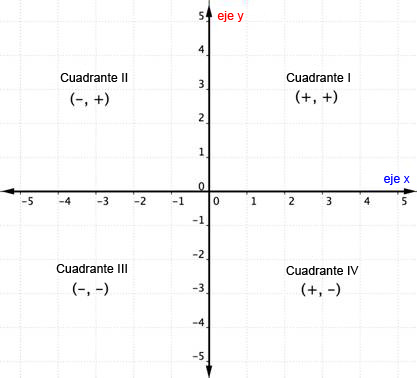
El ejemplo de abajo detalla cómo determinar el cuadrante de un punto sólo pensando en los signos de sus coordenadas. Saber qué cuadrante ocupa el punto te puede ayudar a prevenir un error. También es información útil para comprobar que has graficado el punto correctamente.
| Ejemplo | ||
| Problema | ¿En qué cuadrante se encuentra el punto (−7, 10)? | |
|
| (−7, 10) | Observa los signos de las coordenadas x y y. Para este par ordenado, los signos son (−, +). |
|
| Los puntos con el patrón | Usando la tabla anterior, localiza el patrón (−, +). |
| Respuesta | El punto (−7, 10) está en el Cuadrante II. | |
| Ejemplo | ||
| Problema | ¿En qué cuadrante se encuentra el punto (−10, −5)? | |
|
| (−10, −5) | Observa los signos de las coordenadas x y y. Para este par ordenado, los signos son (−, −). |
|
| Los puntos con el patrón | Usando la tabla anterior, localiza el patrón (−, −). |
| Respuesta | El punto (−10, −5) está en el Cuadrante III. | |
¿Qué pasa si un par ordenado tiene una coordenada x o y de cero? El ejemplo siguiente muestra la gráfica del par ordenado (0, 4).
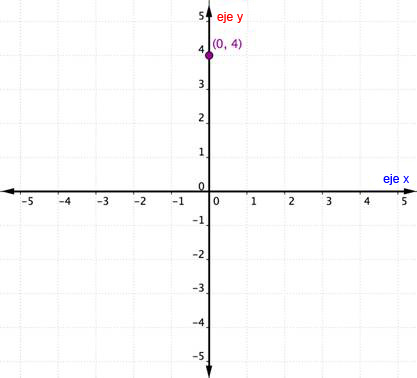
Un punto localizado en uno de los ejes no se considera en un cuadrante. Simplemente está en uno de los ejes. Cuando la coordenada-x es 0, el punto se localiza en el eje-y. De manera similar, cualquier punto que tenga una coordenada-y de 0 estará localizado en el eje-x.
| ¿Cuál de las descripciones siguientes describe mejor la localización del punto (8, 0)?
A) Cuadrante I
B) Está en el eje-x
C) Está en el eje-y
D) El plano de coordenadas
|
Sumario
El plano de coordenadas es un sistema para graficar y describir puntos y rectas. El plano de coordenadas consiste en un eje-x horizontal y un eje-y vertical. La intersección de estas dos rectas crea el origen, que es el punto (0, 0). El plano coordenado se divide en cuatro cuadrantes. Juntas, estas características del sistema de coordenadas permiten una representación gráfica y comunicación sobre puntos, rectas, y otros conceptos algebraicos.