Graficando sistemas de ecuaciones lineales
Objetivos de Aprendizaje
· Resolver un sistema de ecuaciones lineales por medio de una gráfica.
· Determinar si un sistema de ecuaciones lineales es consistente o inconsistente.
· Determinar si un sistema de ecuaciones lineales es dependiente o independiente.
· Determinar si un par ordenado es una solución a un sistema de ecuaciones.
· Resolver problemas de aplicación graficando sistemas de ecuaciones.
Introducción
Recuerda que una ecuación lineal se grafica como una recta, que indica que todos los puntos de una recta son soluciones de la ecuación lineal. Existe un número infinito de soluciones. Si tenemos un sistema de ecuaciones lineales, la solución del sistema es el valor que hace válidas todas las ecuaciones. Para dos variables y dos ecuaciones, este es el punto donde las gráficas se intersectan. Las coordenadas de este punto serán la solución para las dos variables en las dos ecuaciones.
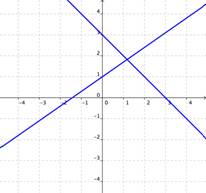
La solución de un sistema de ecuaciones es el valor o valores que hacen válidas a todas las ecuaciones en el sistema. Las gráficas de las ecuaciones del sistema te dicen cuántas soluciones existen para ese sistema. Observa las imágenes siguientes. Cada una muestra dos rectas que forman el sistema de ecuaciones.
| Una Solución | No hay Soluciones | Soluciones Infinitas |
|
|
|
|
| Si las gráficas de las ecuaciones se intersectan, entonces existe una solución que es válida para ambas ecuaciones.
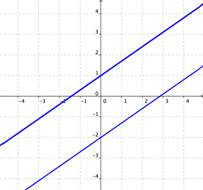
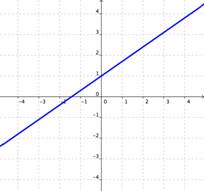
| Si las gráficas de las ecuaciones no se intersectan (por ejemplo, si son paralelas), entonces no existen soluciones que sean válidas para ambas ecuaciones. | Si las gráficas de las ecuaciones son la misma, entonces existe un número infinito de soluciones que son válidas para ambas ecuaciones. |
Cuando las rectas se intersectan, el punto de intersección es el único punto que las dos gráficas tienen en común, Entonces las coordenadas de ese punto son la solución de las dos variables usadas en las ecuaciones. Cuando las rectas son paralelas, no hay soluciones y a veces las dos ecuaciones se grafican como la misma recta, en tal caso tenemos un número infinito de soluciones.
Algunos términos especiales son usados a veces para describir tipos de sistemas.
Los siguientes términos se refieren a cuántas soluciones tiene el sistema.
o Cuando un sistema tiene una solución (las gráficas de las ecuaciones se intersectan), es un sistema consistente de ecuaciones lineales y las ecuaciones son independientes.
o Cuando el sistema no tiene solución (las gráficas de las ecuaciones no se intersectan), es un sistema inconsistente de ecuaciones lineales y las ecuaciones son independientes.
o Si las rectas son la misma (las gráficas se intersectan en todos los puntos), es un sistema consistente de ecuaciones lineales y las ecuaciones son dependientes. Esto es, cualquier solución de una ecuación debe ser también una solución de la otra, por lo que las ecuaciones dependen una de la otra.
Los siguientes términos se refieren a si un sistema tiene soluciones.
o El sistema es un sistema consistente de ecuaciones lineales cuando tiene soluciones.
o El sistema es un sistema inconsistente de ecuaciones lineales cuando no tiene soluciones.
| Podemos resumir esto como sigue: o Un sistema con una o más soluciones es consistente. o Un sistema sin soluciones es inconsistente. o Si las rectas son diferentes, las ecuaciones son ecuaciones lineales independientes. o Si las rectas son iguales, las ecuaciones son ecuaciones lineales dependientes. |
| Ejemplo | ||
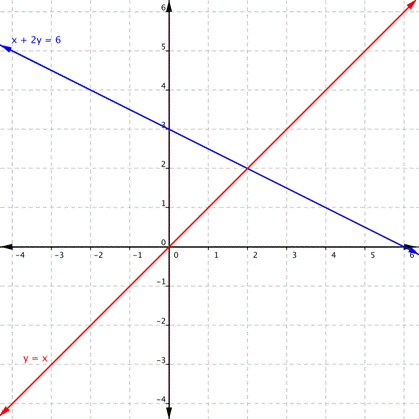
| Problema | Usando la gráficas de y = x y x + 2y = 6, mostrada abajo, determina cuántas soluciones tiene el sistema. Luego clasifica el sistema como consistente o inconsistente y las ecuaciones dependientes o independientes. | |
|
|
Las rectas se intersectan en un punto. Entonces las dos rectas tienen sólo un punto en común, sólo hay una solución para el sistema.
Como las rectas no son la misma, las ecuaciones son independientes.
Como sólo hay una solución, el sistema es consistente.
| |
| Respuesta | El sistema es consistente y las ecuaciones son independientes. | |
| Ejemplo Avanzado | ||
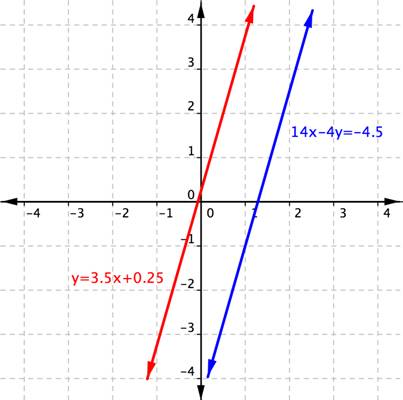
| Problema | Usando la gráficas de y = 3.5x + 0.25 y 14x – 4y = -4.5, mostrada abajo, determina cuántas soluciones tiene el sistema. Luego clasifica el sistema como consistente o inconsistente y las ecuaciones dependientes o independientes. | |
|
| Las rectas son paralelas, lo que significa que no se intersectan. No hay soluciones para el sistema.
Las rectas no son la misma, las ecuaciones son independientes.
No hay soluciones. Entonces, el sistema es inconsistente.
| |
| Respuesta | El sistema es inconsistente y las ecuaciones son independientes. | |
| Pregunta Avanzada ¿Cuáles de las siguientes son ecuaciones dependientes y representan a un sistema consistente?
A)
B)
C)
D)
|
De la gráfica anterior, puedes ver que existe una solución para el sistema y = x y x + 2y = 6. La solución parece ser (2, 2). Sin embargo, debes verificar una solución que encuentras en una gráfica para asegurarte que no es (2.001, 2.001) o (1.9943, 1.9943).
Una manera de verifica que el punto existe en ambas rectas es sustituir los valores de x y y del par ordenado en la ecuación de cada recta. Si la sustitución es un enunciado válido, ¡entonces tienes la solución correcta!
| Ejemplo | |||
| Problema | ¿Es (2, 2) una solución del sistema y = x y x + 2y = 6? | ||
|
| y = x 2 = 2
VÁLIDO
(2, 2) es una solución de y = x. | x + 2y = 6 2 + 2(2) = 6 2 + 4 = 6 6 = 6
VÁLIDO
(2, 2) es una solución de x + 2y = 6. | Como la solución del sistema debe ser una solución para todas las ecuaciones en el sistema, comprueba el punto en cada ecuación. Sustituye 2 por x y 2 por y en cada ecuación. |
| Respuesta | (2, 2) es una solución del sistema. | Como (2, 2) es una solución de cada ecuación en el sistema, (2, 2) es una solución del sistema. | |
| Ejemplo | |||
| Problema | ¿Es (3, 9) una solución del sistema y = 3x y 2x – y = 6? | ||
|
| y = 3x 9 = 3(3)
VÁLIDO
(3, 9) es una solución de y = 3x. | 2x – y = 6 2(3) – 9 = 6 6 – 9 = 6 -3 = 6
INVÁLIDO
(3, 9) no es una solución de 2x – y = 6. | Como la solución del sistema debe ser una solución para todas las ecuaciones en el sistema, comprueba el punto en cada ecuación. Sustituye 3 por x y 9 por y en cada ecuación.
|
| Respuesta | (3, 9) no es una solución del sistema. | Como (3, 9) no es una solución de una de las ecuaciones en el sistema, no puede ser una solución para el sistema. | |
| Ejemplo | |||
| Problema | ¿Es (−2, 4) una solución del sistema y = 2x y 3x + 2y = 1? | ||
|
| y = 2x 4 = 2(−2) 4 = −4
INVÁLIDO
(−2, 4) no es una solución de y = 2x. | 3x + 2y = 1 3(−2) + 2(4) = 1 −6 + 8 = 1 2 = 1
INVÁLIDO
(−2, 4) no es una solución de 3x + 2y = 1. | Como la solución del sistema debe ser una solución para todas las ecuaciones en el sistema, comprueba el punto en cada ecuación. Sustituye −2 por x y 4 por y en cada ecuación.
|
| Respuesta | (−2, 4) no es una solución del sistema. | Como (3, 9) no es solución de ninguna de las ecuaciones en el sistema, (−2, 4) no es una solución para el sistema. | |
Recuerda que para que un valor sea una solución del sistema de ecuaciones, el punto debe ser una solución de ambas ecuaciones. Una vez que encuentras una ecuación en donde el punto es inválido, has determinado que no es una solución para el sistema.
| ¿Cuál de los siguientes enunciados es válido para el sistema 2x – y = −3 y y = 4x – 1?
A) (2, 7) es una solución de una ecuación pero no de la otra, entonces es una solución del sistema.
B) (2, 7) es una solución de una ecuación pero no de la otra, entonces no es una solución del sistema.
C) (2, 7) es una solución de ambas ecuaciones, entonces es una solución del sistema.
D) (2, 7) no es solución de ninguna de las ecuaciones, entonces no es una solución del sistema.
|
La gráfica como método de solución
Puedes resolver gráficamente el sistema. Sin embargo, es importante recordar que debes comprobar la solución, porque podría no ser precisa.
| Ejemplo | |||
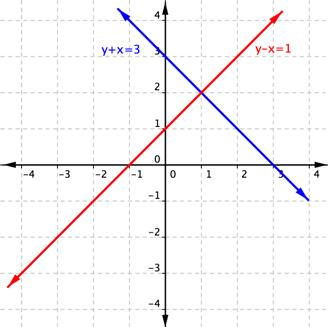
| Problema | Encontrar las soluciones del sistema y – x = 1 y y + x = 3. | ||
|
| Primero, grafíca ambas ecuaciones en los mismos ejes.
Las dos rectas se intersectan, Esto significa que sólo hay una solución en el sistema.
| ||
|
| El punto de intersección parece ser (1, 2). | Lee el punto de la gráfica lo más preciso posible. | |
|
| y – x = 1 2 – 1 = 1 1 = 1
VÁLIDO
(1, 2) es una solución de y – x = 1. | y + x = 3 2 + 1 = 3 3 = 3
VÁLIDO
(1, 2) es una solución de y + x = 3. | Comprueba los valores de ambas ecuaciones. Sustituye 1 por x y 2 por y. (1, 2) es una solución. |
| Respuesta | (1, 2) es una solución del sistema y – x = 1 y y + x = 3. | Como (1, 2) es una solución de cada ecuación en el sistema, es una solución del sistema. | |
| Ejemplo | ||
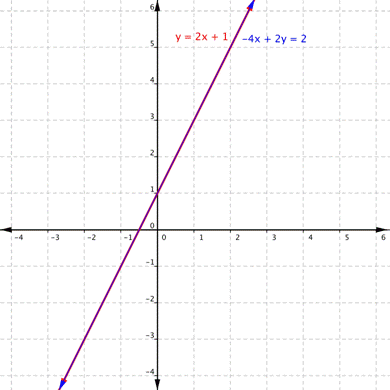
| Problema | ¿Cuántas soluciones tiene el sistema y = 2x + 1 y −4x + 2y = 2? | |
|
|
Primero, grafica ambas ecuaciones en los mismos ejes.
Las dos gráficas son la misma recta. Entonces cada punto en la recta es una solución para el sistema de ecuaciones.
| |
| Respuesta | El sistema y = 2x + 1 y −4x + 2y = 2 tiene un número infinito de soluciones. | |
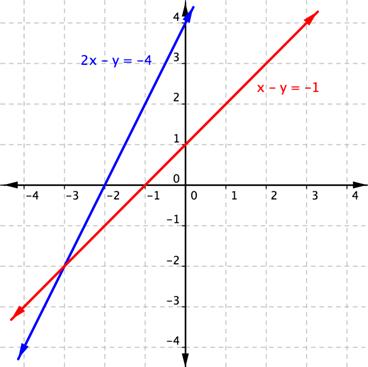
| ¿Qué punto es la solución del sistema x – y = −1 y 2x – y = −4? A continuación se muestra el sistema graficado.
A) (−1, 2)
B) (−4, −3)
C) (−3, −2)
D) (−1, 1)
|
Graficar un sistema de ecuaciones en un contexto del mundo real puede ser útil para visualizar el problema. Veamos un par de ejemplos.
| Ejemplo | |||
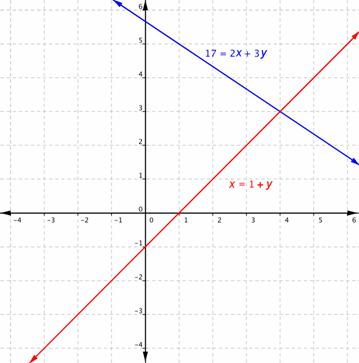
| Problema | En el juego de básquetbol de ayer, Cheryl anotó 17 puntos con una combinación de canastas de 2 y de 3 puntos. El número de tiros de 2 fue uno más que el número de tiros de 3. ¿Cuántas canastas de cada tipo marcó Cheryl? | ||
|
| x = el número de tiros hechos de 2 puntos y = el número de tiros hechos de 3 puntos
| Asigna variables a las cantidades desconocidas – el número de tiros de cada tipo. | |
|
| 2x = el número de canastas de 2 puntos 3y = el número de canastas de 3 puntos
| Calcula cuántos puntos se hacen de cada tipo de tiro. | |
|
| El número de puntos que marcó Cheryl (17) = los puntos de canastas de 2 puntos + los puntos de canastas de 3 puntos.
17 = 2x + 3y | Escribe una ecuación usando la información dad en el problema. | |
|
| El número de canastas de 2 puntos (x) = 1 + el número de canastas de 2 puntos (y)
x = 1 + y | Escribe una segunda ecuación usando la información adicional dada en el problema. | |
|
| 17 = 2x + 3y x = 1 + y | Ahora tienes un sistema de dos ecuaciones con dos variables. | |
|
|
Grafíca ambas ecuaciones en el mismo eje.
Las dos rectas se intersectan, por lo que tienen un punto en común. Esto significa que sólo hay una solución para el problema.
| ||
|
| El punto de intersección parece ser (4, 3). | Lee el punto de intersección en la gráfica. | |
|
| 17 = 2x+ 3y 17 = 2(4) + 3(3) 17 = 8 + 9 17 = 17
VÁLIDO
(4, 3) es una solución de 17 = 2x + 3y. | x = 1 + y 4 = 1 + 3 4 = 4
VÁLIDO
(4, 3) es una solución de x = 1 + y | Comprueba (4, 3) en cada ecuación para ver si es una solución del sistema de ecuaciones.
(4, 3) es una solución de la ecuación.
x = 4 y y = 3 |
| Respuesta | Cheryl hizo 4 canastas de 2 puntos y 3 canastas de tres puntos. | ||
| Ejemplo | ||
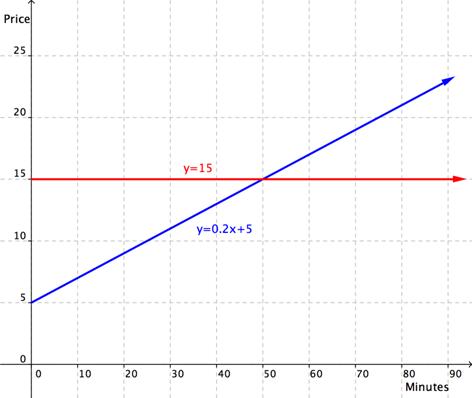
| Problema | Andres está tratando de decidir cuál de los dos planes de telefonía móvil comprar. Un plan, TalkALot, aplica un cargo fijo de $15 al mes por minutos ilimitados. Otro plan, FriendFone, aplica un cargo mensual de $5 además de cobrar 20¢ por minuto de llamada.
Para examinar los planes, Andres hizo una gráfica:
Si él planea hablar por teléfono por unos 70 minutos al mes, ¿cuál es el plan que le conviene comprar? | |
|
|
| Observa la gráfica, TalkALot se representa como y = 15, mientras que FriendFone se representa con y = 0.2x + 5.
El número de minutos está en el eje-x. Cuando x = 70, TalkALot cuesta $15, mientras que FriendFone cuesta unos $19. |
| Respuesta | Andres debería comprar el plan de TalkALot. | Como TalkALot cuesta menos por 70 minutos, Andres debe comprar ese plan. |
Observa que si el estimado fuera incorrecto, se podría hacer un nuevo estimado. Graficando de nuevo acercándose al área donde las rectas se cruzan y hacer una mejor estimación.
| Paco y Lisel gastaron $30 en el cine anoche. Paco gastó $8 más que Lisel.
Si P = es la cantidad que gastó Paco, y L = la cantidad que gastó Lisel, ¿qué sistema de ecuación pues podrías usar para calcular cuánto gastaron cada uno?
A) P + L = 30 P + 8 = L
B) P + L = 30 P = L + 8
C) P + 30 = L P − 8 = L
D) L + 30 = P L − 8 = P
|
Sumario
Un sistema lineal de ecuaciones consiste en dos o más ecuaciones que tienen las mismas variables. Puedes graficar las ecuaciones como un sistema para averiguar si el sistema no tiene soluciones (está representado por rectas paralelas), una solución (representado por rectas que se intersectan), o un número infinito de soluciones (representado por dos rectas que se sobreponen). Si bien los sistemas de ecuaciones en una gráfica son una técnica útil, no siempre son precisas para identificar un punto específico y por lo tanto una solución para un sistema de ecuaciones.